
Wee Annie statue at end of Kempock Street, Gourock, with face mask during COVID-19 pandemic. Photo Dave Ssouza

Wee Annie statue at end of Kempock Street, Gourock, with face mask during COVID-19 pandemic. Photo Dave Ssouza

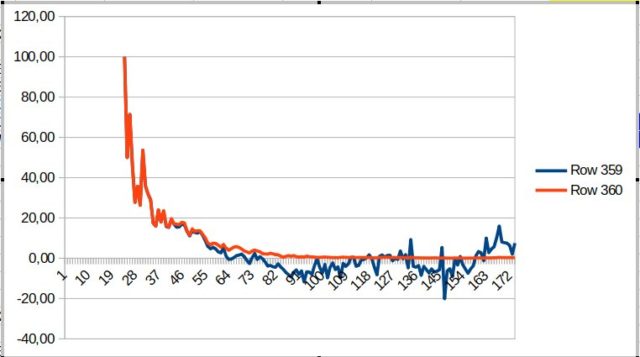
Charts are from 5 Feb until 27 July 2020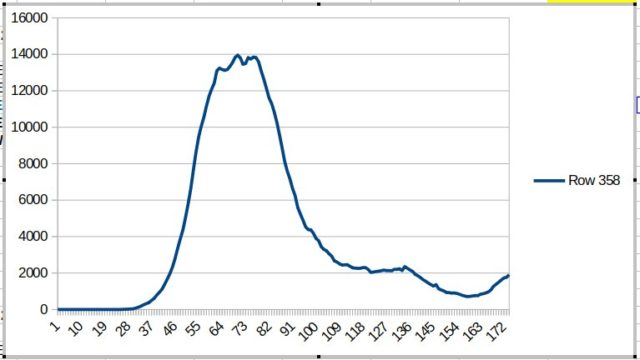



22 juli 2020

22 juli 2020



| # | Country | Inhabitants | Country | Tested positive 8 July 2020 | ‰ (per mille) of population tested positive |
| 1 | Qatar | 2740479 | Qatar | 100945 | 36,83 |
| 2 | Vatican City[note 1] | 453 | Vatican City | 12 | 26,49 |
| 3 | French Guiana (France) | 244118 | French Guiana | 5178 | 21,21 |
| 4 | San Marino | 34641 | San Marino | 713 | 20,58 |
| 5 | Bahrain | 1543300 | Bahrain | 30321 | 19,65 |
| 6 | Chile | 17373831 | Chile | 301019 | 17,33 |
| 7 | Kuwait | 4420110 | Kuwait | 51245 | 11,59 |
| 8 | Andorra | 76177 | Andorra | 855 | 11,22 |
| 9 | Oman | 4645249 | Oman | 48997 | 10,55 |
| 10 | Mayotte (France) | 256518 | Mayotte | 2688 | 10,48 |
| 11 | Armenia | 2957500 | Armenia | 29820 | 10,08 |
| 12 | Peru | 32162184 | Peru | 305703 | 9,51 |
| 13 | Panama | 4158783 | Panama | 39334 | 9,46 |
| 14 | United States | 329997511 | USA | 2923432 | 8,86 |
| 15 | Singapore | 5703600 | Singapore | 45140 | 7,91 |
| 16 | Brazil | 211764774 | Brazil | 1623284 | 7,67 |
| 17 | Luxembourg | 613894 | Luxembourg | 4603 | 7,50 |
| 18 | Sweden | 10343403 | Sweden | 73344 | 7,09 |
| 19 | Belarus | 9397800 | Belarus | 64003 | 6,81 |
| 20 | Moldova | 2681735 | Moldova | 18141 | 6,76 |
| 21 | Maldives | 374775 | Maldives | 2501 | 6,67 |
| 22 | Saudi Arabia | 34218169 | Saudi Arabia | 217108 | 6,34 |
| 23 | Belgium | 11524454 | Belgium | 62123 | 5,39 |
| 24 | United Arab Emirates | 9770529 | UAE | 52600 | 5,38 |
| 25 | Spain | 46934632 | Spain | 252130 | 5,37 |
| 26 | Gibraltar (United Kingdom) | 33701 | Gibraltar | 179 | 5,31 |
| 27 | Ireland | 4921500 | Ireland | 25538 | 5,19 |
| 28 | Iceland | 366130 | Iceland | 1873 | 5,12 |
| 29 | Falkland Islands (United Kingdom) | 2563 | Falkland Islands | 13 | 5,07 |
| 30 | Russia[note 11] | 146877088 | Russia | 700792 | 4,77 |
| 31 | Djibouti | 1078373 | Djibouti | 4878 | 4,52 |
| 32 | Portugal | 10276617 | Portugal | 44416 | 4,32 |
More on the next subpage (click below)
Hij lijkt het weer te doen. In elk geval QSO’s maken lukt gewoon weer, net als Starnetserver PI8XDV.
De komende dagen wordt de rest van de configuratie bij langs gelopen.